Convergence with respect to VTACS multipolar order

05 December, 2023

Objective

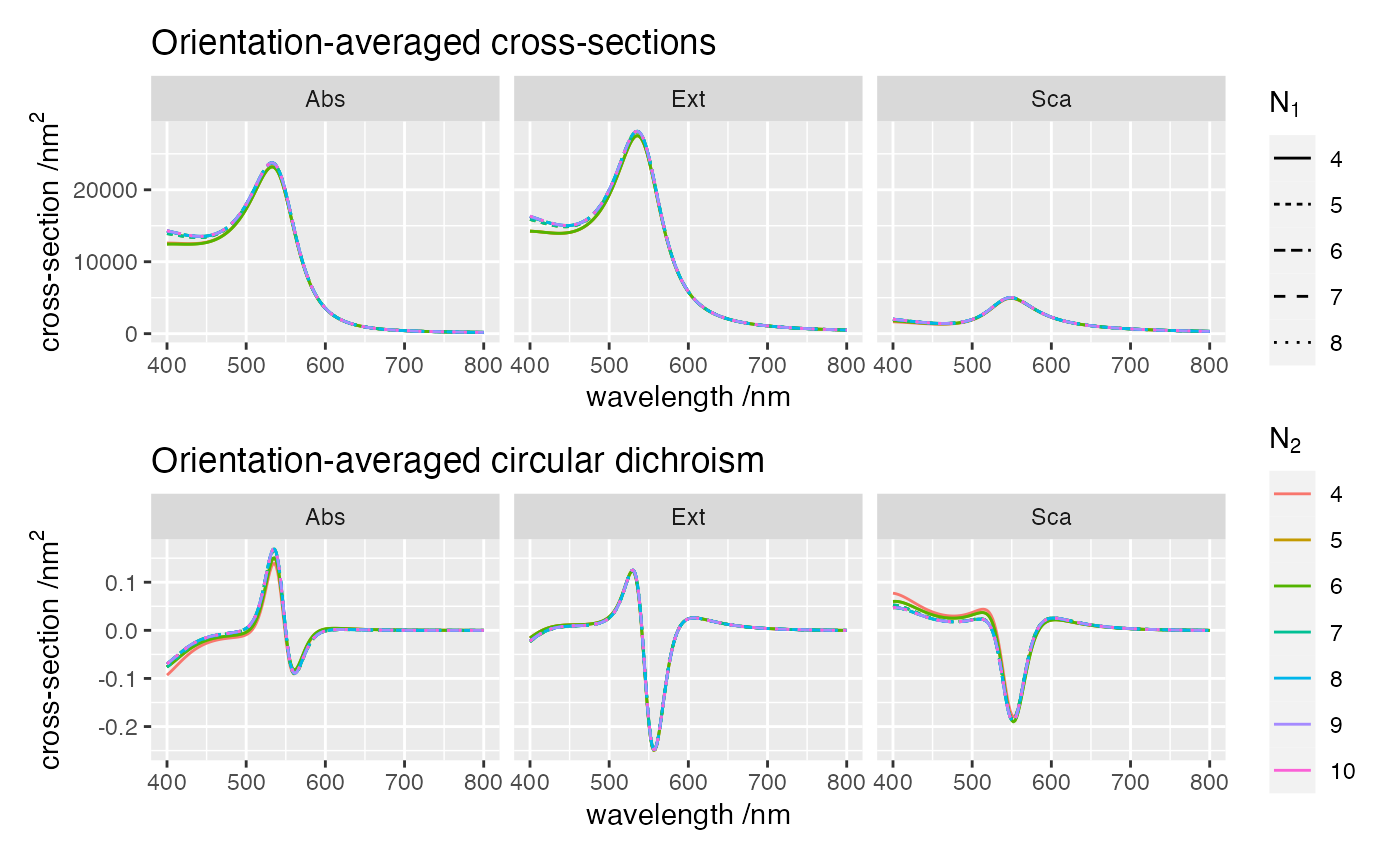
This example checks the convergence of orientation-averaged cross-sections with respect the maximum multipolar order describing individual scatterers and translation of vector spherical waves. The structure consists of four gold spheres in water arranged in a helix.

This simulation uses the following input file

ModeAndScheme 2 3
Wavelength 400 800 200
Medium 1.7689 # epsilon of water
MultipoleSelections 1
EE1:4_EM1:4_ME1:4_MM1:4 blocks
OutputFormat HDF5 cross_sections_{n1}_{n2}

MultipoleCutoff {n1} {n2}

Scatterers 4
Au_S1 200 0 -75 25
Au_S1 161.803398874989 117.557050458495 -25 25
Au_S1 61.8033988749895 190.211303259031 25 25
Au_S1 -61.8033988749895 190.211303259031 75 25

where {n1}, {n2} are replaced by 4,5,... in each separate run.

Orientation-averaged results

We see that in this example the cross-sections require higher than 4 multipolar orders in both \(n_1\) and \(n_2\) to converge, especially at shorter wavelengths. Typically, one needn’t set \(n_2\), as the default value \(n_1=n_2\) is accurate; this optional parameter is mostly a remnant from the initial development stages.

---

Last run: 05 December, 2023