The Kretschmann configuration consists of a thin metal film, typically 50nm of gold or silver, deposited on top of a high-index prism (n=1.5 for glass). Light incident from the prism side undergoes total internal reflection (TIR) above ~45 degrees (internal angle). The evanescent field associated with TIR penetrates the metal and may couple to surface plasmon-polaritons supported at the air/metal interface.

Here we model the optical properties of such a system, starting with the angular variation of the reflectivity.

Reflectivity against internal incident angle for the Kretschmann configuration, at fixed wavelength

Setting up

library(planar)
library(ggplot2)
require(reshape2)
library(gridExtra)
require(plyr)

Modelling the reflectivity

wvl <- 632.8
gold <- epsAu(wvl)
results <- recursive_fresnelcpp(epsilon = list(1.5^2, gold$epsilon, 1), wavelength = gold$wavelength, 
    thickness = c(0, 50, 0), angle = seq(0, pi/2, length = 2000), polarisation = "p")
str(results)

## List of 9
##  $ wavelength  : num 633
##  $ k0          : num 0.00993
##  $ angle       : num [1:2000] 0 0.000786 0.001572 0.002357 0.003143 ...
##  $ q           : num [1:2000] 0 0.000786 0.001572 0.002357 0.003143 ...
##  $ reflection  : cplx [1:2000] -0.599-0.709i -0.599-0.709i -0.599-0.709i ...
##  $ transmission: cplx [1:2000] 0.142-0.122i 0.142-0.122i 0.142-0.122i ...
##  $ R           : num [1:2000] 0.861 0.861 0.861 0.861 0.861 ...
##  $ T           : num [1, 1:2000] 0.0524 0.0524 0.0524 0.0524 0.0524 ...
##  $ A           : num [1, 1:2000] 0.0868 0.0868 0.0868 0.0868 0.0868 ...

Plotting the results

m <- data.frame(results[c("angle", "R")])

tir <- asin(1/1.5) * 180/pi

ggplot(m) + geom_vline(aes(xintercept = x), data = data.frame(x = tir), linetype = 2, 
    color = "grey50") + geom_line(aes(angle * 180/pi, R)) + scale_y_continuous("Reflectivity", 
    expand = c(0, 0), limits = c(0, 1)) + scale_x_continuous("Internal angle /degrees", 
    expand = c(0, 0), breaks = seq(0, 90, by = 15))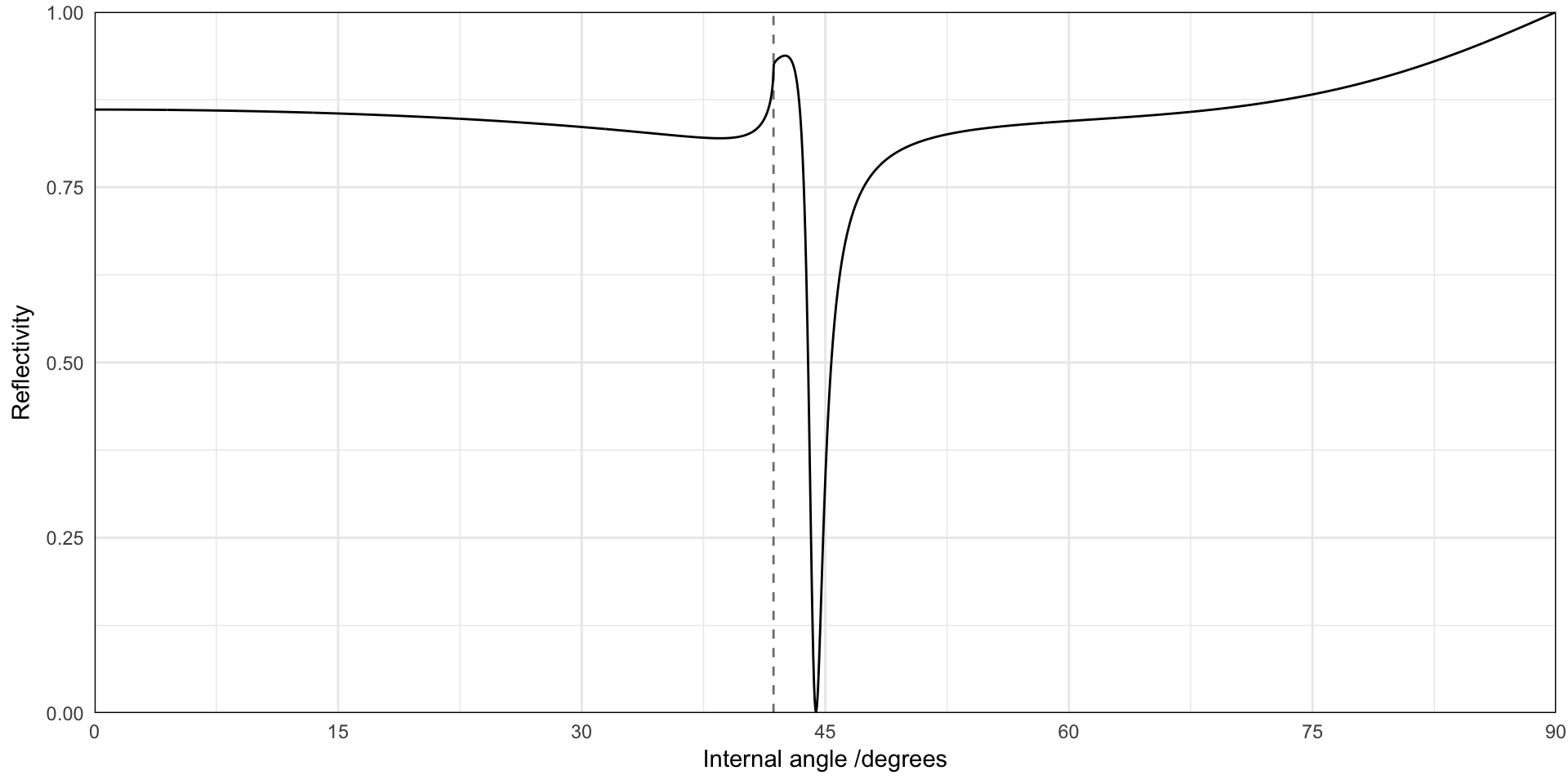

Variation of the parameters, and effect on the resonance

We now look at the effect of changing the thickness of the metal layer, from non-existent (single air/glass interface), to an opaque metal film. First, we wrap the calculation in a function, and loop over this function with a vector of film thicknesses.

simulation <- function(thickness = 50) {
    results <- recursive_fresnelcpp(epsilon = list(1.5^2, gold$epsilon, 1^2), 
        wavelength = gold$wavelength, thickness = c(0, thickness, 0), angle = pi/180 * 
            seq(15, 60, length = 500), polarisation = "p")
    data.frame(results[c("angle", "R")])
    
}

## loop over parameters
parameters <- function(res = 10) data.frame(thickness = seq(0, 100, length = res))

d1 <- mdply(parameters(10), simulation)
d2 <- mdply(parameters(300), simulation)


p1 <- ggplot(d1) + geom_line(aes(angle * 180/pi, R, colour = thickness, group = thickness)) + 
    scale_y_continuous("Reflectivity", expand = c(0, 0), limits = c(0, 1)) + 
    scale_x_continuous("Internal angle /degrees", expand = c(0, 0), breaks = seq(0, 
        90, by = 15)) + guides(colour = guide_legend())

## colour map
p2 <- ggplot(d2) + geom_raster(aes(angle * 180/pi, thickness, fill = R)) + scale_y_continuous("thickness", 
    expand = c(0, 0)) + scale_x_continuous("Internal angle /degrees", expand = c(0, 
    0), breaks = seq(0, 90, by = 15))

grid.arrange(p1, p2, nrow = 2)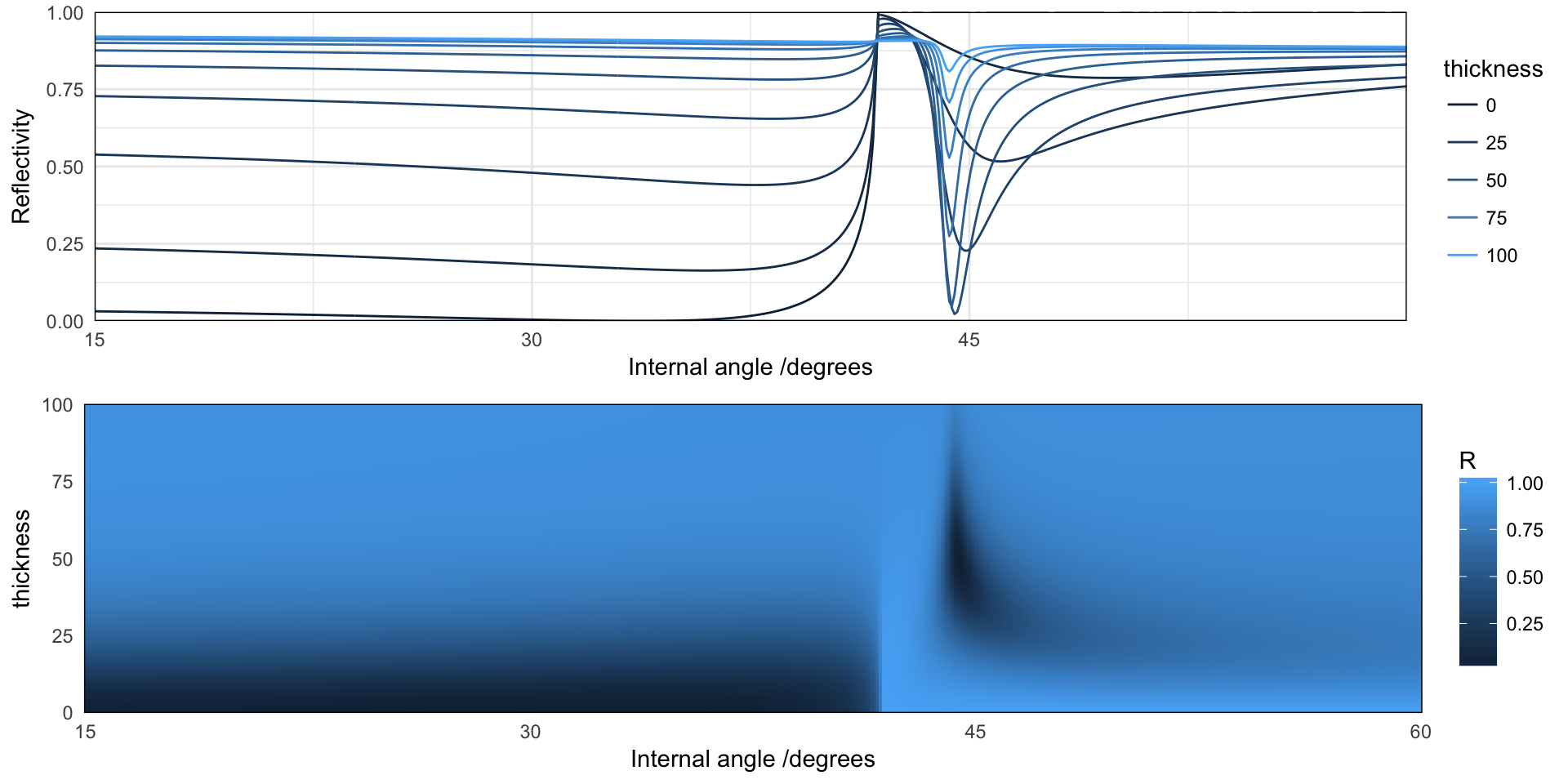

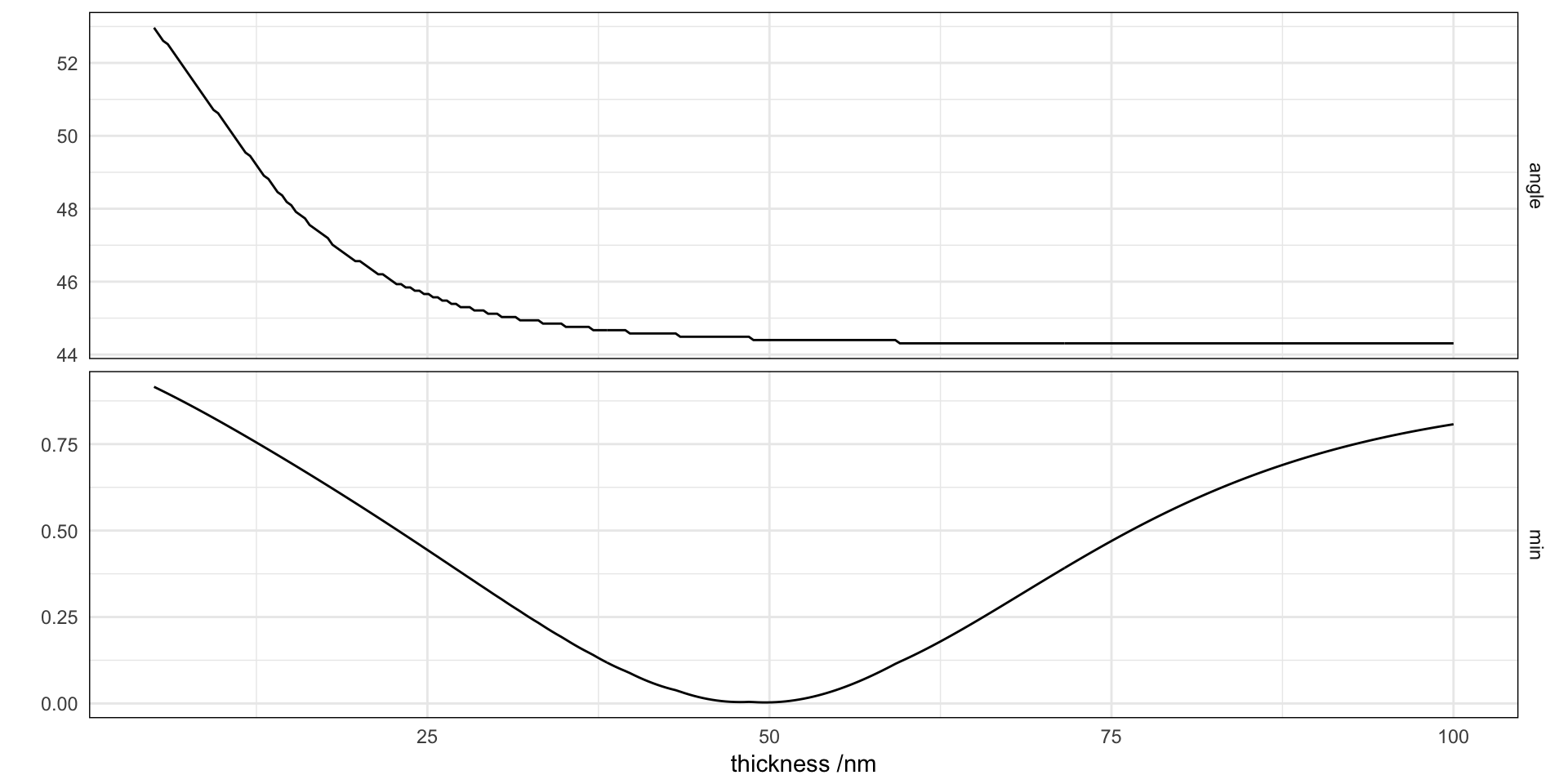
minimum <- ddply(subset(d2, angle > tir * pi/180 & thickness > 5), .(thickness), 
    summarize, angle = angle[which.min(R)] * 180/pi, min = min(R))
ggplot(melt(minimum, id = "thickness")) + facet_grid(variable ~ ., scales = "free") + 
    geom_line(aes(thickness, value)) + labs(y = "", x = "thickness /nm")