Fresnel formulae

Single interface

Let us consider the situation depicted below,

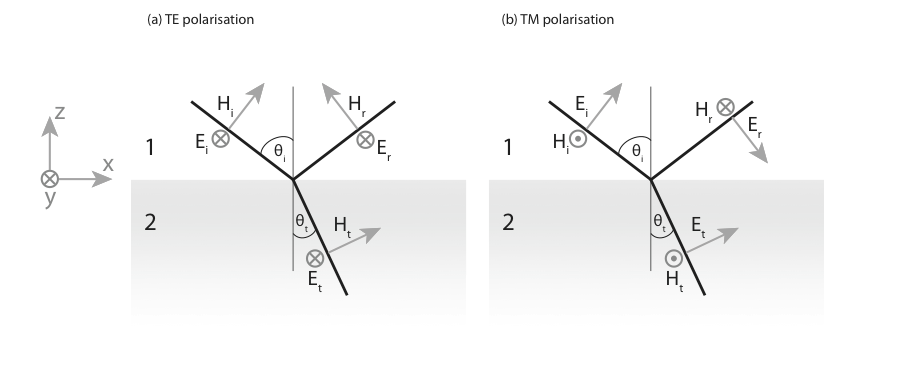
Schematic of reflection and transmission by a single interface. Note that the orientation of the vectors has been chosen so as to have a consistent picture at normal incidence.

where we define the Fresnel coefficients as the ratio of the complex amplitude of the electric fields, $r= E_r/E_i$ for the reflection coefficient, and $t= E_t/E_i$ for the transmission coefficient. The Fresnel coefficients can be obtained by considering the continuity of the tangential component of the $E$ and $H$ fields at the interface. The continuity of the normal components of $D$ and $B$ does not yield supplementary conditions and will not be considered. It is worth noting that the continuity of $H^y$ is only valid for materials that do not sustain a surface current resulting from the addition of external charges.

TE-polarised light

For TE-polarised light, the continuity of $E^y$ reads, $E_i + E_r = E_t$ which yields, $1+r =t.$ The continuity of $H^x$ can be written as, $H_i\cos\theta_i - H_r\cos\theta_i = H_t\cos\theta_t$ It is convenient to express the angles in terms of the normal component of the $k$ -vectors, $k_z = n k_0 \cos\theta.$ for the incident, reflected, and refracted fields, so that $\cos\theta_t / \cos\theta_i=\dfrac{k_{z2}n_1}{k_{z1}n_2}$ . The complex magnitude of the magnetic and electric fields are linked in each medium by the optical impedance. Its expression can be obtained from the induction law in a homogeneous medium, $\nabla\times\mathbf{E} = -\partial_t \mathbf{B}$ expressed in Fourier space as, $\mathbf{k}\times \mathbf{E} = i\omega \mathbf{B}$ The ratio $E/H$ is the impedance, written as, $\frac{E}{H}= c \mu \mu_0 / n= \sqrt{\frac{\mu\mu_0}{\varepsilon\varepsilon_0}}=Z\cdot Z_0.$ We can define the admittance $Y$ as the inverse impedance, $Y=\dfrac{1}{Z\cdot Z_0}$ The continuity of $H^y$ can be expressed as, $Y_1 (1 - r) = Y_2 \frac{n_1k_{z2}}{n_2k_{z1}}t.$ After rearranging, we obtain, $1 - r = \frac{\mu_1k_{z2}}{\mu_2k_{z1}}t.$ We can summarize the two continuity relations in the following system,

$\left\{ \begin{aligned} 1 + r &= t\\ 1 - r &= \frac{\mu_1 k_{z2}}{\mu_2 k_{z1}}t \end{aligned}\right.$ Solving for $r$ and $t$ yields the result, $t_{12}^s=\frac{2\mu_2 k_{z1}}{\mu_2 k_{z1}+\mu_1k_{z2}},\qquad r_{12}^s=\frac{\mu_2 k_{z1}-\mu_1k_{z2}}{\mu_2 k_{z1}+\mu_1k_{z2}}.$

TM-polarised light

For TM-polarised light, it is generally easier to consider the Fresnel coefficients for the magnetic field, denoted $\rho$ and $\tau$ . The continuity of $H^y$ reads, $1 - \rho = \tau$ The continuity of $E^y$ can be written, $\frac{k_{z1}}{\varepsilon_1} + \rho \frac{k_{z1}}{\varepsilon_1} = \tau \frac{k_{z2}}{\varepsilon_2}$

We can summarize the two continuity relations in the following system,

$\left\{ \begin{aligned} 1 - \rho &=\tau\\ (1 + \rho) \frac{k_{z1}}{\varepsilon_1}&=\frac{k_{z2}}{\varepsilon_2}\tau \end{aligned}\right.$ Solving for $\rho$ and $\tau$ yields the result, $\tau_{12}^p=\frac{2\varepsilon_2 k_{z1}}{\varepsilon_2 k_{z1}+\varepsilon_1k_{z2}},\qquad \rho_{12}^p=\frac{\varepsilon_2 k_{z1}-\varepsilon_1k_{z2}}{\varepsilon_2 k_{z1}+\varepsilon_1k_{z2}}.$

To summarize, for a single interface from 1 to 2 with normal along the $z$ direction, the Fresnel coefficients read, $\begin{aligned} \rho_{12}^p&=\frac{\varepsilon_2 k_{z1}-\varepsilon_1k_{z2}}{\varepsilon_2 k_{z1}+\varepsilon_1k_{z2}},&{}& r_{12}^s=\frac{\mu_2 k_{z1}-\mu_1k_{z2}}{\mu_2 k_{z1}+\mu_1k_{z2}}\\ \tau_{12}^p&=\frac{2\varepsilon_2 k_{z1}}{\varepsilon_2 k_{z1}+\varepsilon_1k_{z2}},&{}& t_{12}^s=\frac{2\mu_2 k_{z1}}{\mu_2 k_{z1}+\mu_1k_{z2}}. \end{aligned}$

Note that, $r_{ij}=-r_{ji}.$ To verify the conservation of energy, one must consider the irradiance defined in terms of the electric field as $I=\frac{1}{2}Y|E|^2$ , yielding, $R=\frac{I_r}{I_i}=|r|^2, \qquad T=\frac{I_t}{I_i}=\frac{Y_1}{Y_2}|t|^2.$ and we can verify that, indeed, $R+T=1$ for a single interface.

Reflectivity of a layer

From the viewpoint of ray optics, a thin layer will support an infinite number of internal reflections (absorption and irregularities will however reduce the intensity in a physical situation). The infinite series of reflected orders can be expressed in the form a geometric sum, leading to a closed form formula as shown below.

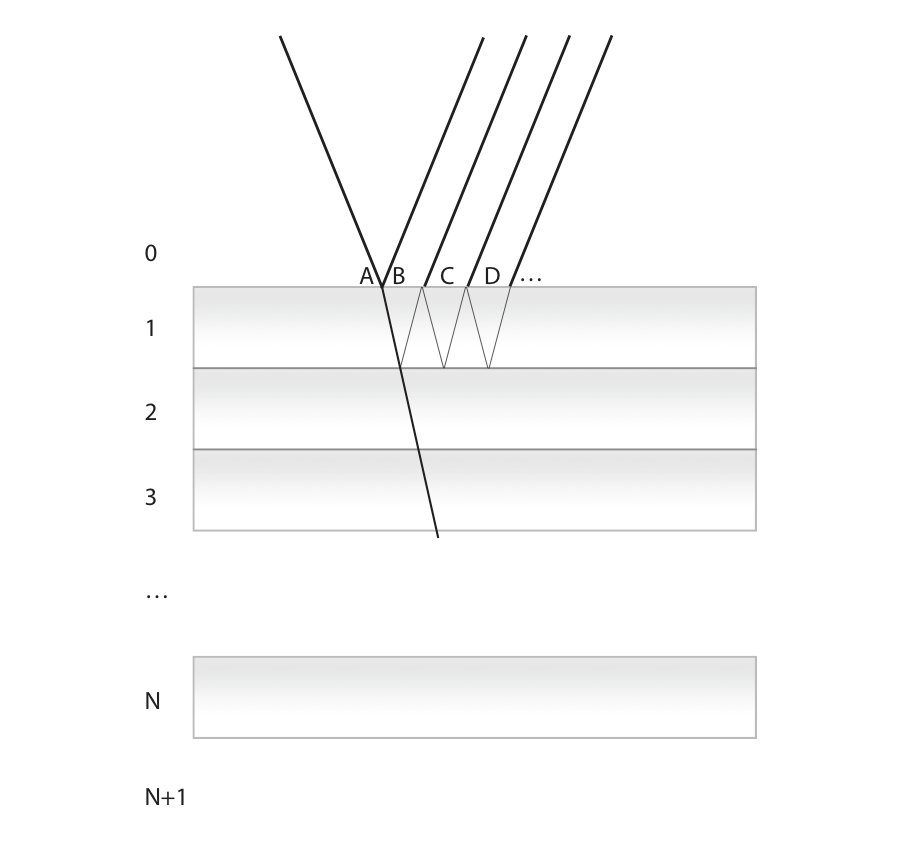
Schematic of reflection and transmission by a multilayer stack. A few reflected orders are noted A, B, C and D for the first film.

An incident plane wave with amplitude $A$ impinges on the first interface. It can be reflected, $B=r_{01}A$ , or transmitted. The total response of the slab can be obtained by following each order of reflection inside the slab (C, D, $\dots$ ).

Upon transmission at the first interface, the wave amplitude is $t_{01}A$ . Application of Fermat’s principle yields a phase change $\Delta \phi= k_{z1}d$ when the wave hits the second interface. The reflection coefficient at this interface is $r_{12}$ . The partial wave reflected from this path, noted C, is therefore $C=t_{10}t_{01}r_{12}\exp(2i k_{z1}d)A$ .

Similarly, in D, $D=t_{10}t_{01}r_{10}r_{12}^2\exp(4i k_{z1}d)A$ And, for the ${j^\text{th}}$ partial wave, $t_{10}t_{01}r_{12}^{j}r_{10}^{{j-1}}\exp(2i {j}k_{z1}d)A$ The wave reflected by the slab is the sum of these contributions, $r_{\text{slab}}A=B+C+D+\dots=\left[r_{01}+t_{10}t_{01}r_{12}\sum_{j=0}^{\infty}r_{12}^jr_{10}^{j}\exp(2ji k_{z1} d)\right]A$ For clarity, I write $\beta=r_{12}r_{10}\exp(2i k_{z1}d)$ . The summation of all partial waves is thereby expressed as a geometrical sum, $r_{\text{slab}}=r_{01} + \left(t_{10}t_{01}r_{12}\exp(2i k_{z1}d)\right)\sum_{j=0}^{\infty}\beta^j$ Recalling that the sum of a geometric series of common ratio $q$ is $\frac{1}{1-q}$ , we can write, $r_{\text{slab}}=r_{01} + \frac{t_{10}t_{01}r_{12}\exp(2i k_{z1}d)}{1-r_{12}r_{10}\exp(2i k_{z1}d)}$

We note that for either polarisation we have the following identity, $t^s_{ij}t^s_{ji} = (1-r^s_{ij})(1+r^s_{ij})= 1-(r^s_{ij})^2 ,\qquad t^p_{ij}t^p_{ji} =\frac{Y_i}{Y_j}(1-r^p_{ij})\frac{Y_j}{Y_i}(1+r^p_{ij}) = 1-(r^p_{ij})^2$ Using this equation and the substitution $r_{10} = -r_{01}$ we finally obtain, $r_{\text{slab}}=\frac{r_{01}+r_{12}\exp(2i k_{z1}d)}{1+r_{01}r_{12}\exp(2i k_{z1}d)}.$

For the transmission, one obtains,

$t_{\text{slab}}=\frac{t_{01}t_{12}\exp(i k_{z1}d)}{1+r_{01}r_{12}\exp(2i k_{z1}d)}.$

Reflectivity of a multilayer structure

When N layers are stacked together, the reflection coefficient of the structure can be found by applying recursively the preceding formula for a single layer. This amounts to considering one of the reflection coefficients to be the effective reflection accounting for all the layers behind. Let us consider explicitly the case of a 3 layer system. The procedure is as follows,

Compute and store for later use all single-interface coefficients, namely $r_{01}$ , $r_{12}$ , $r_{23}$ , $r_{34}$
Combine the previous coefficients to compute the reflectivity of the last layer, i.e. $r_{24} = \frac{r_{23}+r_{34}\exp(2i k_{z3}d_3)}{1+r_{23}r_{34}\exp(2i k_{z3}d_3)}$ . This value can be stored in a temporary variable $r_{\text{tmp}}$
Go up, combining one interface at a time, $r_{\text{tmp}}=r_{14} = \frac{r_{12}+r_{24}\exp(2i k_{z2}d_2)}{1+r_{12}r_{24}\exp(2i k_{z2}d_2)}$
the combined reflectivity of the multilayer is obtained when one has reached the top interface, $r_{\text{tmp}} = r_{04} = \frac{r_{01}+r_{14}\exp(2i k_{z1}d_1)}{1+r_{01}r_{14}\exp(2i k_{z1}d_1)}$

baptiste Auguié

04 March, 2017

Single interface

TE-polarised light

TM-polarised light

Reflectivity of a layer

Reflectivity of a multilayer structure

Contents